Two Body Problem

• 

Kepler

1. Planet orbits follow an Ellipse
2. Motion of planets carve out equal area in ellipses per unit time
   • $A_1=A_2$ for fixed $\Delta t$
3. Period of motion is related to semi-major axis (SMA)
   • $p^2\approx a^3$
4. Geometric Solution to 2BP
   • $r\cos \left(\theta \right)=\frac{p}{1+e\cos \left(\theta \right)}$

Newton

Creates Calculus

• Builds derivatives off of ratios: $\frac{\Delta r}{\Delta t}\to \vec{r}\to \frac{\mathrm{d}\vec{r}}{\mathrm{d}\vec{t}}\to \frac{{\mathrm{d}}^2\vec{r}}{\mathrm{d}{t}^2}$

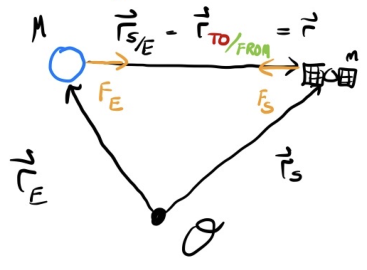
1. Computes forces:
   • $\overrightarrow{F_E}=\frac{GMm}{r^2}\hat{r}$
   • $\overrightarrow{F_S}=\frac{GMm}{r^2}\left(-\hat{r}\right)$
2. Compute acceleration:
   • $\vec{F}=m\vec{a}=m\ddot{\vec{r}}\to \ddot{\vec{r}}=\frac{\vec{F}}{m}$
   • $\ddot{\overrightarrow{r_E}}=\frac{Gm}{r^2}\hat{r}$
   • $\ddot{\overrightarrow{r_S}}=-\frac{GM}{r^2}\hat{r}$
3. Subtract accelerations to find relative motion:
   • $\ddot{\overrightarrow{r_E}}-\ddot{\overrightarrow{r_S}}=-\frac{G(M+m)}{r^2}\hat{r}$
4. Assume $m\ll M$:
   • $G(M+m)\approx GM=\mu$

Validating K2

• Using the triangle small angle approximation:
  • Area of triangle: $\frac{LW}{2}$
  • $L\approxeq |r|$
  • $W\approxeq |v|\sin \left(\theta \right)\mathrm{d}t$
  • $\mathrm{d}A=\frac{|r||v|\sin \left(\theta \right)\mathrm{d}t}{2}$
  • $\frac{\mathrm{d}A}{\mathrm{d}t}=\frac{\vec{r}\times \vec{v}\sin \left(\theta \right)}{2}=\frac{|\vec{h}|}{2}$
• If Kepler’s second law holds, then $\frac{\mathrm{d}A}{\mathrm{d}t}$ will be $0$
  • $\left(A_1=A_2⟺\frac{\mathrm{d}A}{\mathrm{d}t}=0\right)$
  • $\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\mathrm{d}A}{\mathrm{d}t}\right)\stackrel{?}{=}0⟹\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\vec{r}\times \vec{v}}{2}\right)=\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\vec{r}\times \dot{\vec{r}}}{2}\right)$
  • $\to -\frac{1}{2}\frac{M}{r^2}\vec{r}\times \hat{r}=0$
  • $⟹\dot{\vec{h}}=0$, and thus angular momentum does not change

Move from 2D to 3D

• Define Polar Bases using Cartesian Basis Vectors
  • $\hat{r}=\cos \left(\theta \right)\hat{x}+\sin \left(\theta \right)\hat{y}$
  • $\hat{\theta }=-\sin \left(\theta \right)\hat{x}+\cos \left(\theta \right)\hat{y}$
• Define position, $\vec{r}$, and velocity, $\dot{\vec{r}}$, in polar coordinates
  • $\vec{r}=r\hat{r}$
  • $\dot{\vec{r}}=r\hat{r}+r\dot{\theta }\hat{\theta }$
• Compute magnitude of $|\vec{h}|$
  • $|\vec{h}|=|\vec{r}\times \dot{\vec{r}}|=\dots =r^2\dot{\theta }$

Validating K1

1. $$\begin{array}{rl}\ddot{\vec{r}}\times \vec{h}& =\left(-\frac{M}{r^2}\hat{r}\right)\times \left(r^2\dot{\theta }\hat{h}\right)\\ & =-M\dot{\theta }\vec{\hat{r}}\times \vec{\hat{h}}\\ & =+M\dot{\theta }\hat{\theta }\\ & =M\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\vec{r}}{r}\right)\end{array}$$
2. $$\begin{array}{rl}\ddot{\vec{r}}\times \vec{h}& \stackrel{?}{=}\frac{\mathrm{d}}{\mathrm{d}t}\left(\dot{\vec{r}}\times \vec{h}\right)\\ & =\ddot{\vec{r}}\times \vec{h}+\vec{r}\times \dot{\vec{h}}\\ \dot{\vec{h}}& =0\\ ⟹\ddot{\vec{r}}\times \vec{h}& =\frac{\mathrm{d}}{\mathrm{d}t}\left(\dot{\vec{r}}\times \vec{h}\right)\end{array}$$
3. Put $\boxed{1}$ and $\boxed{2}$ together
   • $$\begin{array}{rl}\frac{\mathrm{d}}{\mathrm{d}t}\left(\dot{\vec{r}}\times \vec{h}\right)& =\mu \frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\vec{r}}{r}\right)\\ \frac{\mathrm{d}}{\mathrm{d}t}\left(\dot{\vec{r}}\times \vec{h}-\mu \frac{\vec{r}}{r}\right)& =\vec{0}\end{array}$$

Quick sidebar for some questions

• What do we know about $\vec{B}$?

  • Constant of motion
  • In the plane of motion

• What don’t we know about $\vec{B}$?

  • Where is it pointing?
  • Is there a meaningful geometric analog?

• Where is $\vec{B}$ wrt. $\vec{r}$?

  • $$\begin{array}{rl}\vec{r}\cdot \vec{B}& =\vec{r}\cdot \left(\vec{v}\times \vec{h}-\mu \frac{\vec{r}}{r}\right)\end{array}$$
  • $$\begin{array}{rl}r|\vec{B}|\cos \left(\theta \right)& =\vec{r}\cdot \vec{v}\times \vec{h}-\mu \frac{\vec{r}\cdot \vec{r}}{r}\\ & =\dots \\ r|\vec{B}|\cos \left(\theta \right)& =h^2+\mu r\end{array}$$

• This gives:

  • $$r=\frac{\frac{h^2}{\mu }}{1+\frac{|\vec{B}|}{\mu }\cos \left(\theta \right)}$$
  • Newton’s “Calculus” thing might actually work!

4. Compare physical quantities with geometric:

   • $$p=\frac{h^2}{\mu }✓$$
   • $$e=\frac{|\vec{B}|}{\mu }✓$$

5. Tie up loose ends by defining eccentricity vector:

   • $$\vec{e}=\frac{\vec{B}}{\mu }=\frac{\vec{v}\times \vec{h}}{\mu }-\frac{\vec{r}}{r}=e{\hat{i}}_e$$
   • Upon inspection of the ellipse image, $\vec{e}$ lies on the semi-major axis and points to periapsis
   • Like with $\vec{h}$, we want to know about $\vec{e}$
     • $$\begin{array}{rl}E& =KE+U\\ & =\frac{1}{2}m{v}^2-\frac{GMm}{r}\\ ϵ& =\frac{E}{m}=\frac{v^2}{2}-\frac{\mu }{r}\\ & =\dots \\ ϵ& =-\frac{\mu }{2a}\end{array}$$

Using this information

Vis-Viva Equation

• $$\begin{array}{rl}\frac{v^2}{2}-\frac{\mu }{r}=& -\frac{\mu }{2a}\\ ⟹& \boxed{v^2=\mu \left(\frac{2}{r}-\frac{1}{a}\right)}\end{array}$$
• Means that if we know position on the elliptical orbit, we immediately know the velocity (and vice-versa)
• We can simplify beyond to only need $\theta$
• $$\begin{array}{rl}{v}^2=& \mu \left(\frac{2}{\left(\frac{p}{1+e\cos \left(\theta \right)}\right)}-\frac{1}{a}\right)\\ =& \dots \\ ⟹& \boxed{v=\frac{\mu }{h}\sqrt{1+2e\cos \left(\theta \right)+e^2}}\end{array}$$

Prediction

Motivation

• Newton wasn’t happy with being able to describe the motion, he wanted to predict the motion
• Want: $\mathrm{r}\left(\theta \right),\mathrm{v}\left(\theta \right)\to \mathrm{r}\left(t\right),\mathrm{v}\left(t\right)$
• This way, we can know where the planets will be at some $\Delta t$ in the future

Creating the prediction model

• $$\begin{array}{rl}h& =r\theta \\ & =\dots \\ {\int }_{t_0}^{t_1}h\mathrm{d}t& ={\int }_{{\theta }_0}^{{\theta }_1}\frac{p^2}{{\left(1+e\cos \left(\theta \right)\right)}^2}\mathrm{d}\theta \\ {\int }_{t_0}^{t_1}\sqrt{\frac{\mu }{p^3}}\mathrm{d}t& ={\int }_{{\theta }_0}^{{\theta }_1}\frac{1}{{\left(1+e\cos \left(\theta \right)\right)}^2}\mathrm{d}\theta \end{array}$$
• Oh my! That doesn’t look fun to integrate (especially if you just invented calculus and are the only one on the planet who knows integration)
• Let’s think:
  • Question: Is there a more integration-friendly way to represent/model this motion?
  • Answer: Yes! Let’s use the eccentric anomaly of the ellipse
• Let’s rederive $\vec{h}$ using Eccentric Anomaly
  • $$\begin{array}{rl}\vec{r}& =x{\hat{i}}_e+y{\hat{i}}_p\\ \dot{\vec{r}}& =\dot{x}{\hat{i}}_e+\dot{y}{\hat{i}}_p\\ \vec{h}& =\vec{r}\times \dot{\vec{r}}\\ & =\dots \\ \vec{h}& =\left(x\dot{y}-\dot{x}y\right){\hat{i}}_h\end{array}$$
  • $$\begin{array}{rl}\mathrm{x}\left(E\right)& =a\left(\cos \left(E\right)-e\right)\\ \mathrm{y}\left(E\right)& =a\sqrt{1-e^2}\sin \left(E\right)\\ \dot{\mathrm{x}}\left(E\right)& =-a\sin \left(E\right)\frac{\mathrm{d}E}{\mathrm{d}t}\\ \dot{\mathrm{y}}\left(E\right)& =a\sqrt{1-e^2}\cos \left(E\right)\frac{\mathrm{d}E}{\mathrm{d}t}\end{array}$$
• Plug into $|\vec{h}|$

Kepler's Formula

• $$\begin{array}{rl}\vec{h}=& \left(x\dot{y}-\dot{x}y\right){\hat{i}}_h\\ =& \dots \\ \sqrt{\frac{\mu }{a^3}}=& \left(1-e\cos \left(E\right)\right)\frac{\mathrm{d}E}{\mathrm{d}t}\\ =& \dots \\ ⟹& \boxed{\sqrt{\frac{\mu }{a^3}}\left(t_1-t_0\right)=E-e\sin \left(E\right){]}_{E_0}^{E_1}}\end{array}$$