Reference Frames

• We care about more than 1-D and 2-D problems
• We need tools for more complex positions & motion
• This is where reference frames come in

Basics

• 
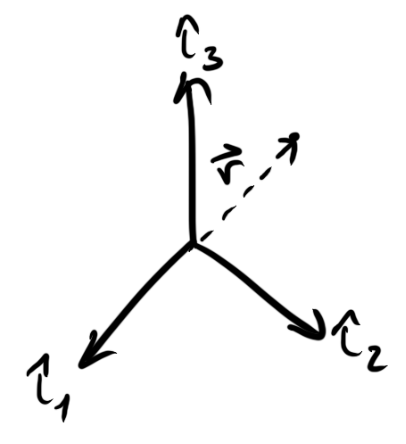
• A Reference Frame is a set of basis vectors which we used to describe our problem
• Imagine an arbitrary reference frame, $\mathcal{I}$:
  • $$\mathcal{I}=\left\{{\hat{i}}_1,{\hat{i}}_2,{\hat{i}}_3\right\}$$
• For $\vec{r}$ in the $\mathcal{I}$ frame:
  • $${}^{\mathcal{I}}\vec{r}=3{\hat{i}}_1+4{\hat{i}}_2+5{\hat{i}}_3$$
• We can also make a new frame, $\mathcal{E}$:
  • $$\mathcal{E}=\left\{{\hat{e}}_1,{\hat{e}}_2,{\hat{e}}_3\right\},\text{ where }{\hat{e}}_2\equiv \vec{r}$$
• $\vec{r}$ in this new frame:
  • $$\begin{array}{rl}{}^{\mathcal{E}}\vec{r}& =0{\hat{e}}_1+9{\hat{e}}_2+0{\hat{e}}_3\\ & =9{\hat{e}}_2\end{array}$$

Polar 2BP

• 

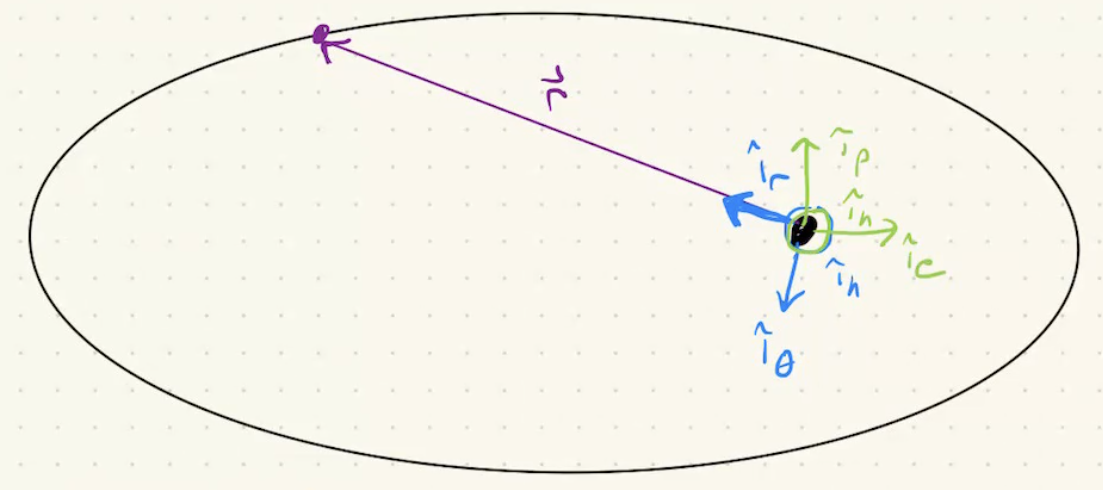
Orbit Frame

• $$\mathcal{O}=\left\{{\hat{i}}_r,{\hat{i}}_{\theta },{\hat{i}}_h\right\}$$
• $${}^{\mathcal{O}}\vec{r}=r{\hat{i}}_r$$
• Pro: Very easy to represent position
• Con: Hard to represent velocity
  • Have to do partial derivatives, as components of the position vector depend on each other
  • $$\frac{\mathrm{d}}{\mathrm{d}t}\left({}^{\mathcal{O}}\vec{r}\right)=\dot{r}{\hat{i}}_r+r\frac{\mathrm{d}}{\mathrm{d}t}\left({\hat{i}}_r\right)$$

Perifocal Frame

• Alternative to Orbit Frame
• $$\mathcal{P}=\left\{{\hat{i}}_e,{\hat{i}}_p,{\hat{i}}_h\right\}$$
• Unfortunately, position vector looks ugly D:
• However, velocity vector is easily calculable in this frame :D
• $$\begin{array}{rl}{}^{\mathcal{P}}\vec{r}& =r\left(\cos \left(\theta \right){\hat{i}}_e+\sin \left(\theta \right){\hat{i}}_p\right)\\ & =\frac{p}{1+e\cos \left(\theta \right)}\left(\cos \left(\theta \right){\hat{i}}_e+\sin \left(\theta \right){\hat{i}}_p\right)\\ {}^{\mathcal{P}}\vec{v}& =\frac{\mathrm{d}}{\mathrm{d}t}\left({}^{\mathcal{P}}\vec{r}\right)\\ & =\sqrt{\frac{\mu }{p}}\left(-\sin \left(\theta \right){\hat{i}}_e+\left(e+\cos \left(\theta \right)\right){\hat{i}}_p\right)\end{array}$$

Types of Reference Frames

Non-Inertial

• Rotating frame
• Basis vectors are constantly changing
• Example: Orbital Frame

Inertial

• Non-Rotational Frame
• Basis vectors don’t change
• Example:
  • Perifocal Frame
  • $${\hat{i}}_e{|}_{t=0}={\hat{i}}_e{|}_{t=t_0+\Delta t}$$

Reference Frames for Earth

• $$\begin{array}{rl}\mathcal{E}& =\left\{{\hat{e}}_1,{\hat{e}}_2,{\hat{e}}_3\right\}\\ {\hat{e}}_3& =\text{Rotation Axis of Earth and Pole}\\ {\hat{e}}_1& =\text{Equator}+0^{\circ }\text{Longitude}\\ {\hat{e}}_2& ={\hat{e}}_3\times {\hat{e}}_1\end{array}$$
• $\mathcal{E}$ is the Earth Centered, Earth Fixed (ECEF) Reference Frame